Everybody (& nature) wants to maximize something (money, satisfaction, disorder, etc..) while minimizing certain others (work, loss, etc..). Hence, Physics & many other subjects require the idea of maxima, minima & inflection. The following material is NOT a rigorous proof, but serves as a quick reference- along with some memory tips- of their conditions.
A) Without extrema or inflection
TIP: You cannot balance a ball anywhere.
B) With extrema or inflection
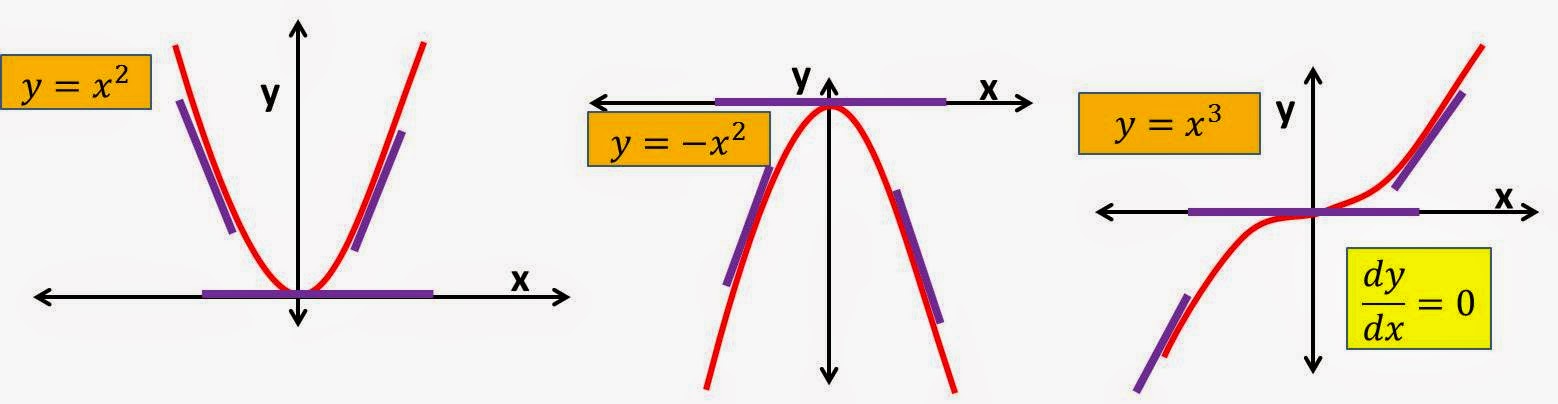
If the first derivative is ZERO at a point, then it is either an extrema (maxima or minima) or a point of inflection. (Here, it is at x=0)
TIP: Violet, thick lines are the tangents to the curves at different points. Observe that their slope is zero at the points of extrema or inflection (at x=0). You can balance a ball only at these points.
B.1) With extrema
If the first derivative is ZERO at a point & the next non-zero derivative is an even derivative, then that point is an extrema. It can be a maxima or a minima.
B.1.1) With minima
If the first derivative is ZERO at a point & the next non-zero
derivative is an even derivative and is positive then that point is a minima.
TIP: The second derivative tells about how the first derivative is going
to increase or decrease after the extremum point. Hence, if it is
positive, it means that the slope is going to increase at the next point. i.e
you were already at the minima.
B.1.1) With maxima
If the first derivative is ZERO at a point & the next non-zero derivative is an even derivative and is negative then that point is a maxima.
TIP: The second derivative tells about how the first derivative is going to increase or decrease after the extrimum point. Hence if it is negative, it says that the slope is going to decrease at the next point. i.e you were already at the maxima.
B.2 With inflection
If the first derivative is ZERO at a point & the next non-zero
derivative is an odd derivative, then that point is a point of inflection.
